|
Chapter 1. Basic Principles
of Political Phenomena
A. General Principles of Political
Phenomena
(3) Basic Theory of Mathematical
Politics
a. Change of Survival Capacity and
Political Profit
 If
we understand survival directivity as survival expansion,
then we can find a quantitative aspect here. As a
result, we can start by quantitatively describing
political phenomena and explaining them using mathematical
models. Understanding political phenomena through
mathematical models is not always necessary, but it
will be better if we can also understand them in this
way, along with other methods.
Let me introduce the concept of 'capacity'( )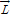
for a quantitative description of a survival process.
This will be a basic unit to quantify political phenomenon.
Survival capacity
Here, every capacity()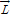
is a survival capacity, and it represents 'everything
a human being needs for their own survival'. A human
being needs several things at least for their survival,
so a survival capacity is composed of several factors.
The symbol '',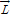
which describes a capacity, is described as a 'vector'.
According to the principle of Samjae
capacities[Ch.1.2], I will assume its elements are
3. (Afterwards, I will express this as simply 'L',
unless I need to use exact mathematical concepts.)
In conclusion, survival capacity
is a vector like the following.
Here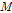 
represents an armed capacity, 
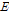represents an economic capacity, and  represents
an ideological capacity. An increase in this survival
capacity()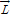
is a profit, and a decrease in survival capacity is
a loss. Every vector ( ,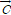
 ,
 ,
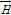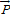etc.) that will be introduced afterwards is nothing
more than another symbol for survival capacity .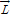
It is not possible to always accurately
measure the various tangible and intangible elements
included in survival capability, but it is possible
to perceive them quantitatively to some extent. As
seen in the saying "losing money is losing less,
but losing honor is losing more", many people
also speak of intangible capacities such as honor
as being "much" or "little".
Now, if the concept of survival capacity
is used to express survival directivity, the following
formalization can be done using the concept of survival
expansionism[Tab.1.1](c).
| |
[Ch.1.3] Every individual( )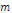
strive to maximize the size of their survival
capacity(). |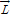
This sentence is the basic premise
in all discussions that explain the political phenomenon
as a mathematical model.
In the mathematical model that describes
the political phenomenon, I represent political actors
as political capacities, which directly describe political
power and the actual political changes. This is similar
to energy being equivalent to work in physics. Bill
Gates, a global billionaire, has much greater political
influence than a person who earns $50 thousand annually.
His political power comes from the size of his wealth
and also functions politically. Similarly, the nuclear
weapons held by the US and Russia have strong military
capacities, which are also political power and trigger
political phenomena.
Change of political profit
According to the principle of survival
expansion[Tab.1.1]¨±, the choices and actions of people
in political phenomena can be seen as a process of
choosing advantageous things (benefits) for survival
and avoiding disadvantageous things (losses). To mathematically
model such political behavior, a model expressing
changes in survival capacity must be established.
The key content is as follows.
| |
[Ch.1.4] Every political
actor changes in the course of paying political
cost(: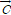
loss) and obtaining political harvest(: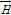
benefit). |
In politics, just like in economic
activities, people incur costs in the process of increasing
their profits. Costs are equivalent to losses. Therefore,
no matter how much one promises loyalty and emphasizes
duty, there will be no one who would be loyal to a
king who has nothing to offer. This is a law that
is maintained everywhere, East or West, Past and Present.
In the 13th century, in England,
when King Edward I raised taxes such as the subsidy
to finance massive war expenses, clergymen and great
lords began to resist because the benefits from obedience
became smaller than the cost of taxes. In the 18th
century, during the Qing Dynasty, when the financial
situation became difficult due to rising prices, government
officials started to bribe the emperor to ease their
finances, which allowed them to extract more money
through illegal and corrupt means. After the American
Revolution, women's right to participate was recognized,
but it was also a choice made considering the increase
in female labor force and expansion of power of certain
political parties.
Here, it is important to remember
that the survival capacity, which is the basic value
of profit and cost, is a three-factor vector based
on the principles of the Samjae capacity[Ch.1.2].
If only considering the single factor of economic
capacity, the behavior of a faithful person who shows
loyalty even without material benefits may not appear
as a behavior that seeks greater benefits than costs,
but if all three capacities are considered, that behavior
can be explained as a behavior that incurs material
costs and chooses ethical benefits. In this context,
it can explain why merchants in Europe around 1000
AD gave their wealth to local influential people under
the guise of protection fees, or why religious followers
donated their wealth to religious institutions and
obtained peace of mind. (If considering the three
capacities still does not support the statement in
[Ch.1.4], then there must be enough examples of political
actors who have no dignity (ideological capacity)
and no means (armed capacity or economic capacity)
to engage in political behavior.)
All people strive for an increase
in their survival capacity, but sometimes it fails.
However, it is certain that people's survival capacity
changes. This applies not only to individuals but
also to larger political actors such as political
organizations. Let's try to express this change in
a mathematical model.
The survival capacity()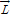
of a political actor changes depending on the payment
of political costs()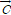
and the obtainment of benefits()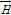
for it.
This can be written in the following
equation.
| |
[Fmla.1.2] (Changhoo
Equation) |
|
The direct meaning of the Changhoo
equation is that the final survival capacity ()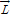
is the result of adding the political cost and benefit
over time from the individual's survival capacity
(: initial value) at a given point, starting from
that point.
On the other hand, political benefit()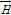
minus political cost()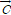
results in 'political profit()'.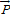
That is,
By combining the two equations above,
the Changhoo equation can be expressed more simply
as follows.
<Every footnote was
deleted from the book>
  
|
To the Top
