|
II-3.
프라이어의 양상 논리
II-3.1. 프라이어의 시제 논리 체계들
프라이어의 양상 논리의 토대는 시제논리 체계이다. 그러므로 시제 논리에 대한
형식적 의미론의 체계를 고찰한 내용에 기초해서 양상논리 의미론의 발전과정을 추적해야만 한다. 적어도
프라이어가 양상논리의 가능세계 의미론에 기여한 부분은 이런 방식으로 탐구하는 것이 적절할 것이다.
프라이어[1968]가 제시한 시제 논리 체계들에는 여러 가지가 있는데 모두
시제 논리 연산자 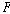 와 와
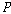 를
기본적으로 사용한다. 그 중에서 를
기본적으로 사용한다. 그 중에서 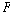 는
미래시제 연산자이고 “…일 것이다(it will be the case that)”를 의미하며 는
미래시제 연산자이고 “…일 것이다(it will be the case that)”를 의미하며 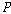 는
과거시제 연산자이고 “…이었다(it has been the case that)”를 의미한다. 한편 는
과거시제 연산자이고 “…이었다(it has been the case that)”를 의미한다. 한편 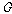 는 는
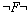 의
약칭이고 의
약칭이고 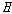 는 는
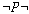 의
약칭이며, 각각 “항상 …일 것이다”(it is always going to be the case that)와
“언제나 …이었다”(it has always been the case that)를 의미한다. 그 밖의
기호들은 고전적인 명제논리와 양화논리의 관례를 따른다. 의
약칭이며, 각각 “항상 …일 것이다”(it is always going to be the case that)와
“언제나 …이었다”(it has always been the case that)를 의미한다. 그 밖의
기호들은 고전적인 명제논리와 양화논리의 관례를 따른다.
프라이어[1968]가 논의하거나 제시하는 시제 논리의 체계들은 크게 i)
기본 시제 논리 체계 ��B와 ii) 양화 시제 논리체계
��Q21),
그리고 iii) 계량 시제 논리(metric tense logic) ��M로
구분될 수 있다.
<기본
시제 논리 ��B>
��B란 원초적 연산자로서 미래
시제 연산자 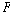 와
과거 시제 연산자 와
과거 시제 연산자 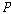 가
도입되어 “ 가
도입되어 “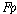 ”와
“ ”와
“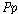 ”
형식의 문장들이 부가된 명제 연산을 가리킨다. 이 때 시제 연산자 ”
형식의 문장들이 부가된 명제 연산을 가리킨다. 이 때 시제 연산자 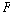 와 와
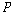 의
뒤에는 바른식 의
뒤에는 바른식 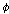 만이
뒤따름으로써 바른식이 이루어진다. 그 각각의 의미는 다음과 같다. 만이
뒤따름으로써 바른식이 이루어진다. 그 각각의 의미는 다음과 같다.
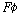 : :
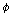 라는
일이 있을 것이다.(It will bee the case that 라는
일이 있을 것이다.(It will bee the case that 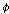 ) )
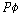 : :
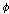 라는
일이 있었다.(It has been the case that 라는
일이 있었다.(It has been the case that 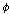 ) )
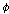 가
“카르납 교수가 달로 날아가고 있다(Professor Carnap is flying to the moon)”라는
명제라고 하자. 이럴 경우 가
“카르납 교수가 달로 날아가고 있다(Professor Carnap is flying to the moon)”라는
명제라고 하자. 이럴 경우 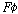 는
“카르납 교수가 달로 날아가는 일이 있었을 것이다(It will be the case that Professor
Carnap is flying to the moon)”가 되고, 는
“카르납 교수가 달로 날아가는 일이 있었을 것이다(It will be the case that Professor
Carnap is flying to the moon)”가 되고, 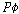 는
“카르납 교수가 달로 날아가는 일이 있었다(It has been the case that Professor
Carnap is flying to the moon)”가 된다. 는
“카르납 교수가 달로 날아가는 일이 있었다(It has been the case that Professor
Carnap is flying to the moon)”가 된다.
��B의 한 예는 레몬(E.
J. Lemmon)의 최소 시제 논리(minimal tense logic) 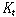 이다. 이다.
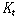 에는
논리적 상항으로서 에는
논리적 상항으로서 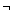 , ,
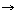 ,
미래시제 연산자 ,
미래시제 연산자 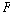 (at
some future time), 그리고 과거시제 연산자 (at
some future time), 그리고 과거시제 연산자 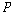 (at
some past time)가 있으며, 다음과 같은 공리들을 가지고 있다. (다음에서 (at
some past time)가 있으며, 다음과 같은 공리들을 가지고 있다. (다음에서 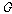 는 는
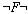 의
약칭이고 의
약칭이고 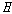 는 는
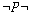 의
약칭이다.) 의
약칭이다.)
(PC1) 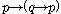
(PC2) 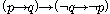
(PC3) 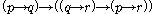
(Kt4) 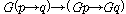 , ,
(Kt5) 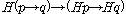 , ,
(Kt6) 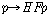 , ,
(Kt7) 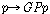
이 중에서 (PC1)-(PC3)의 세 공리는 명제연산의 공리들이다. 그리고
다음의 규칙들이 포함된다.
(Kt8) 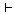 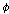 이고 이고
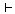 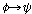 이면 이면
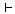 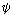 이다. 이다.
(Kt9) 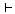 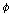 이면 이면
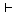 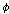 의
임의의 대치 사례이다. 의
임의의 대치 사례이다.
(Kt10) 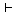 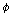 이면 이면
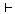 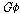 이다. 이다.
(Kt11) 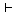 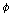 이면 이면
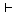 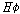 이다. 이다.
어떤 체계 ��가 시제 논리인 경우 그 경우에만
��는 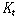 의
언어이고 ��의 공리들과 규칙들이 (PC1)-(PC3), (Kt4)-(Kt7)의
공리들과 (Kt8)-(Kt11)의 규칙들을 포함한다.(Lemmon, 토마슨[1972]) (PC1)-(PC3),
어떤 체계 ��에 있는 (Kt4)-(Kt7)의 공리들과 (Kt8)-(Kt11)
이외의 공리들과 규칙들은 그 체계 ��에 “고유한(proper)” 공리들과
규칙들이라 불린다. 의
언어이고 ��의 공리들과 규칙들이 (PC1)-(PC3), (Kt4)-(Kt7)의
공리들과 (Kt8)-(Kt11)의 규칙들을 포함한다.(Lemmon, 토마슨[1972]) (PC1)-(PC3),
어떤 체계 ��에 있는 (Kt4)-(Kt7)의 공리들과 (Kt8)-(Kt11)
이외의 공리들과 규칙들은 그 체계 ��에 “고유한(proper)” 공리들과
규칙들이라 불린다.
��B에 대한 모형이론적 의미론(MTS)에는
2차 술어적 의미론과 1차 술어적 의미론이 있다.
<��에
대한 2차 술어적 의미론>
��0에 대한 2차 술어적 의미론에서
틀(structure, 혹은 frame)은 순서쌍 <��, 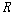 >이고,
여기서 ��는 비공집합이며 >이고,
여기서 ��는 비공집합이며 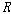 은
��에 대한 순서 관계이다. 은
��에 대한 순서 관계이다. 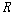 이
순서 관계이므로 이
순서 관계이므로 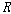 은
곧 2항 관계이다. 관계 은
곧 2항 관계이다. 관계 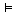 는
할당들(assignments)의 관점에서 정의된다. 즉 ��를 명제적 변항들의
집합이라 하고 는
할당들(assignments)의 관점에서 정의된다. 즉 ��를 명제적 변항들의
집합이라 하고 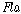 를
식들의 집합이라 하자. 그러면 할당은 함수 를
식들의 집합이라 하자. 그러면 할당은 함수 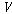 :�� :��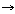 2��이다.
그리고 2��이다.
그리고 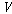 가
어떤 할당이면 가
어떤 할당이면 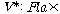 ��
��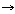 {��,
��}는 다음과 같이 정의된다. {��,
��}는 다음과 같이 정의된다.
(ss1) 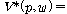 �� ��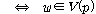
(ss2) 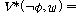 �� ��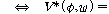 �� ��
(ss3) 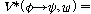 �� ��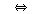 [ [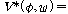 �� ��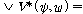 ��] ��]
(ss4) 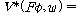 �� ��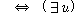 [ [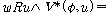 ��] ��]
(ss5) 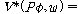 �� ��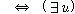 [ [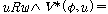 ��] ��]
그렇다면 모든 할당 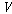 와
모든 와
모든 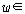 ��에
대하여 ��에
대하여 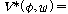 ��일
때 <��, ��일
때 <��, 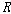 > >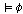 이다.
여기서 ��는 모든 시간들의 집합에 대응되고 이다.
여기서 ��는 모든 시간들의 집합에 대응되고 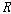 은
시간적 순서에 대응된다. 은
시간적 순서에 대응된다.
2차 술어적 의미론은 시제 논리의 근저에 있는 직관을 명료하게 형식화하는
것으로 보인다. 그럼에도 불구하고 다음에서 고찰될 1차 술어적 의미론이 요구되는 이유가 있다. 그것은
2차 의미론이, 시간의 끝이 있음을 형식화하는 시제 논리체계와 같은, 어떤 흥미로운 시제 논리에 부적절한
것이기도 하다.(Thomason[1972]) 하지만 그보다는 1차 술어적 의미론의 관점은 그 자체로
고찰의 가치가 있고, 또한 프라이어가 시제 논리의 의미론으로서 어떤 고찰을 했는지를 살펴볼 때 시제
연산자가 명제를 1차 술어적 대상으로서 다루고 있다고 생각한 것으로 보이는 부분이 있기 때문이다. 즉
1차 술어적 의미론에서 시제 연산자는 명제를 1차 술어적 대상으로서, 즉 논의영역의 한 원소인 대상으로서
취급한다.
<��에
대한 1차 술어적 의미론>
토마슨(Thomason[1972])은 ��에 대한
1차 술어적 의미론을 다음과 같이 제시한다.22)
여기에서 틀(structure)은 삼중체 <��, 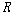 ,
��>인데 ,
��>인데 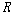 은
비 공집합 ��에 대한 2항 관계이고 ��는 ��의
부분집합들의 비공집합인 집합(collection)이며 불 연산들 및 다음과 같이 정의된 연산들 은
비 공집합 ��에 대한 2항 관계이고 ��는 ��의
부분집합들의 비공집합인 집합(collection)이며 불 연산들 및 다음과 같이 정의된 연산들 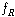 과 과
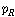 에
닫혀 있다. 에
닫혀 있다.
(fs1) 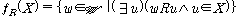
(fs2) 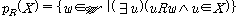
값할당은 이제 함수 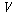 :
�� :
��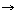 ��이고,
다시 ��이고,
다시 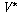 는
(ss1)-(ss5)에 의해 정의되며, <��, 는
(ss1)-(ss5)에 의해 정의되며, <��, 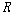 ,
��> ,
��>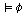 인
그 경우에만 모든 값할당 인
그 경우에만 모든 값할당 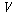 와
모든 와
모든 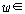 ��에
대해 ��에
대해 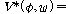 ��이다.
2차 구조 <��, ��이다.
2차 구조 <��, 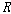 >이
1차 구조 <��, >이
1차 구조 <��, 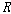 ,
2�� >와 동등하다는 것과 ,
2�� >와 동등하다는 것과 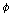 가
<��, 가
<��, 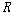 >에서
타당할 때마다 >에서
타당할 때마다 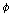 는
어떤 ��에 대해서도 <��, 는
어떤 ��에 대해서도 <��, 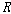 ,
��>에서 타당하다는 것은 분명하다. ,
��>에서 타당하다는 것은 분명하다.
그런데 이렇게 토마슨[1972]이 제시한 형태에서는 ��에
대한 1차 술어적 의미론이 2차 술어적 의미론과 너무나 다른 방식으로 기술되어 있어서 그 차이점과 유사점을
인식하기가 곤란하다. 따라서 2차 술어적 의미론과 최대한 유사한 방식으로 1차 술어적 의미론을 재형식화해
보는 것이 비교 고찰에 있어서 도움이 될 것이다. 그 내용은 다음과 같다.
<1차
의미론의 재형식화>
��에 대한 1차 의미론에서 틀은 삼중체 <��,
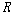 ,
��>인데 여기서 ��는 비공집합이며 ,
��>인데 여기서 ��는 비공집합이며 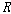 은
비 공집합 ��에 대한 2항 관계이고 ��는 ��의
부분집합들의 비공집합인 집합(collection)이다. 관계 은
비 공집합 ��에 대한 2항 관계이고 ��는 ��의
부분집합들의 비공집합인 집합(collection)이다. 관계 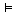 는
할당들(assignments)의 관점에서 정의된다. 즉 ��를 명제적 변항들의
집합이라 하고 는
할당들(assignments)의 관점에서 정의된다. 즉 ��를 명제적 변항들의
집합이라 하고 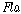 를
식들의 집합이라 하자. 그러면 할당은 함수 를
식들의 집합이라 하자. 그러면 할당은 함수 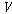 :�� :��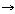 ��이다.
그리고 ��이다.
그리고 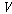 가
어떤 할당이면 가
어떤 할당이면 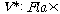 ��
��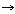 {��,
��}는 다음과 같이 정의된다. 먼저 {��,
��}는 다음과 같이 정의된다. 먼저 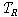 을
다음과 같이 정의하자. 을
다음과 같이 정의하자.
(Df1) 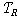 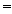 {< {<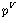 , ,
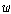 >| >|
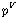 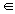 ��, ��,
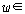 ��} ��}
(fsd1) 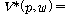 �� ��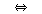
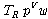
(fsd2) 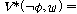 �� ��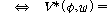 �� ��
(fsd3) 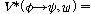 �� ��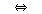 [ [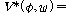 �� ��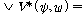 ��] ��]
(fsd4) 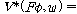 �� ��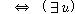 [ [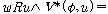 ��] ��]
(fsd5) 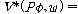 �� ��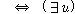 [ [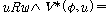 ��] ��]
그렇다면 모든 할당 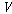 와
모든 와
모든 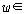 ��에
대하여 ��에
대하여 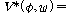 ��일
때 <��, ��일
때 <��, 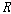 > >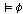 이다. 이다.
이상의 내용에서 1차 술어적 의미론과 2차 술어적 의미론의 차이점은 매우
작아 보인다. 이것은 실질적으로, ��를 개체들의 집합으로 간주하고 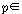 ��에
��의 부분집합을 할당하는 것과 동일하다. 따라서 관계 ��에
��의 부분집합을 할당하는 것과 동일하다. 따라서 관계 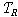 이
두 논항 이
두 논항 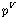 와 와
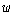 가 가
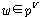 의
관계에 있음을 기술한다고 한다면 두 의미론의 실질적 차이는 사라지는 듯하다. 하지만 그렇더라도 양자의
형식적 차이는 여전히 남아 있다. 의
관계에 있음을 기술한다고 한다면 두 의미론의 실질적 차이는 사라지는 듯하다. 하지만 그렇더라도 양자의
형식적 차이는 여전히 남아 있다.
두 의미론의 좁힐 수 없는 형식적 차이를 확인하고자 한다면 메타 술어인 (Df1)의
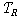 을
2차 술어적 의미론에서 형식화해 보면 된다. 2차 술어적 의미론에서 을
2차 술어적 의미론에서 형식화해 보면 된다. 2차 술어적 의미론에서 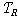 은
다음과 같이 정의되며 이것이 유일한 정의방식이다. 은
다음과 같이 정의되며 이것이 유일한 정의방식이다.
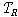 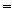 <{ <{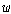 | |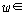 ��}, ��},
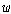 > >
하지만 1차 술어적 의미론에서 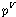 와 와
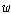 의
관계는 보다 유연하다. 즉 술어 의
관계는 보다 유연하다. 즉 술어  가
집합과 항의 관계를 기술하는 술어가 아닐 수 있으며 어떤 임의적인 2항 관계라도 표상할 수 있다. 가
집합과 항의 관계를 기술하는 술어가 아닐 수 있으며 어떤 임의적인 2항 관계라도 표상할 수 있다.
|